Contact Angle Prediction

In this repository two machine learning algorithms are used for estimating the contact angle of a droplet on a surface from a set of images. Files are orgnized as follows:

Creation of an image dataset in the file $\textit{dataset.py}$, those images are then blurred and augmente in the file $\textit{blurred.py}$. The combination of these two form the train dataset for a machine learning algorithm. Examples of $\textbf{Convolutional Neural Network}$ and $\textbf{Random Forest}$ are respectively in $\textit{detectCA.py}$ and $\textit{RFca.py}$ files. The blender file $\textit{droplet.blend}$ can be used for the test, it generates a set of images that are then pre-processed in the file $\textit{crop}$ _ $lines.py$. The file $\textit{contact}$ _ $angles.py$ contains the calculation of the exact contact angles for each image of the test set. For both the training and the test of the two machine learning algorithms all images are associated with the relative contact angles.

The dataset for the $\textit{training}$ is generated by the file $\textit{dataset.py}$. Starting with the base range of 178 different straight lines representing diffent angles (exluding $0^{\circ}$ and $180^{\circ}$), the program creates 3 set of images with 20 $\times$ 20 pixels focus area in which the Contact Angle location moves in a range from 7 to 14 pixels on the horizontal axis. In this way we get $7\times178=1246$ diffrent images. For each image has been applied an averaging filter kernel of three different sizes. The whole dataset is so composed by,

1246 $\times$ 3 blurred images + 1246 starting images = 4984

The $\textit{test}$ set is generated using the open-source software $\textbf{Blender}$. The file $\textit{droplet.blend}$ creates a 2D animation of a sphere changing shape while dropping into a plane, this represents a raw approximation of a droplet falling on a surface. The animation is composed by 200 frame. This dataset has been used for the test. Following parameter are used to calculate the exact contact angle for each blender image.

$\textbf{rx}$ the semi-major axis

$\textbf{ry}$ the semi-minor axis

$\textbf{a}$ Perpendicular to semi-major axis to the point where the droplet meet the surface.

$\textbf{b}$ Perpendicular to semi-minor axis to the point where the droplet meet the surface (value assumed 1).

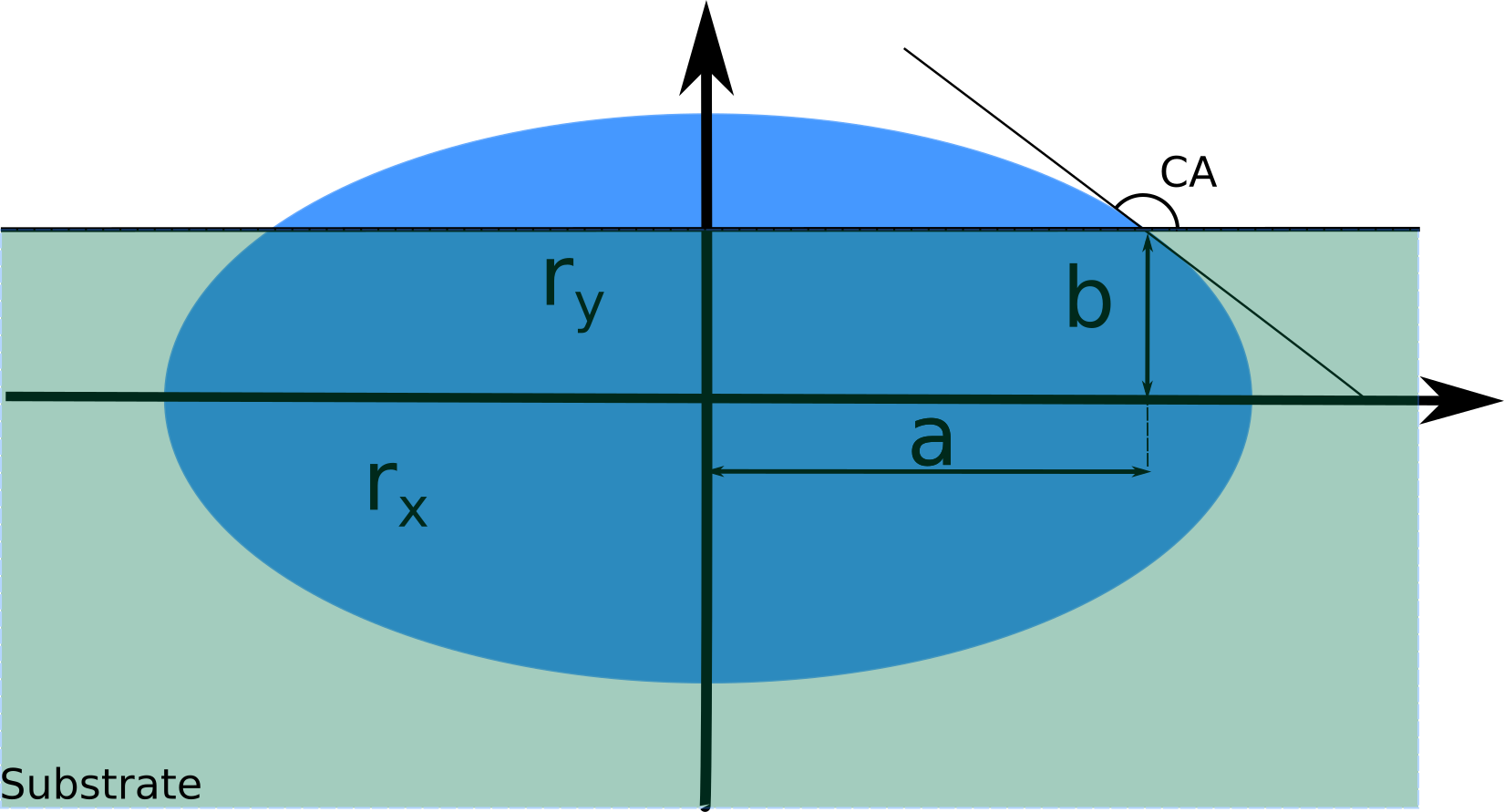
The Ellipse equation can be written as

$$ \begin{equation} \frac{a^2}{{r_x}^2}+\frac{b^2}{{r_y}^2} = 1 \end{equation} $$

In order to calculate the Contact Angle $\textit{CA}$ we can write

$b = \sqrt{{r_y}^2-{r_y}^2\frac{a^2}{{r_x}^2}}$,
$\frac{db}{dx} = -\frac{{r_y}^2 a}{{r_x}^2 \sqrt{{r_y}^2-{r_y}^2\frac{a^2}{{r_x}^2}} }$,
$\frac{db}{dx}(a) = slope$,
$tg(slope) = \textit{CA}$.

Clearly $a = r_x \Rightarrow CA = 90^{\circ}$, also when the ellipse (the droplet) is above $r_y/2, \quad CA = 180^{\circ} - CA$.