Di program ini terdapat beberapa penyelesaian untuk Knapsack Problem, antara lain ada :
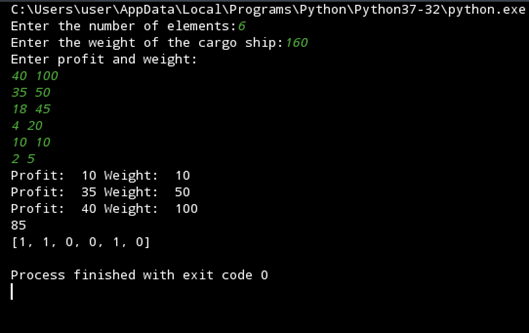
Contoh Permasalahan yang ingin dipecahkan sebagai berikut :
Berat/weight benda = {100, 50, 45, 20, 10, 5}
Nilai kegunaan/values benda= {40, 35, 18, 4, 10, 2}
Dari berbagai benda diatas kita harus menentukan barang terbaik apa yang harus kita bawa/ambil dengan maksimal berat yang dapat dibawa adalah 160
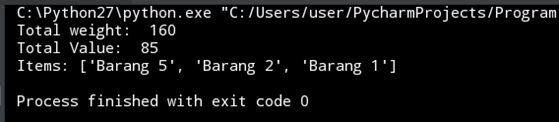
Dengan output sebagai berikut :
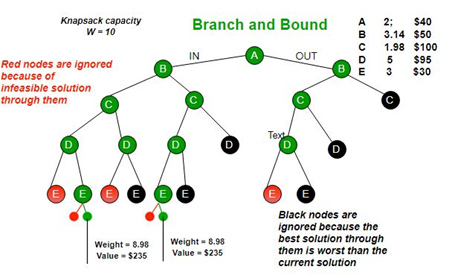
Metode Branch and Bound adalah sebuah teknik algoritma yang secara khusus mempelajari bagaimana caranya memperkecil Search Tree menjadi sekecil mungkin. Sesuai dengan namanya, metode ini terdiri dari 2 langkah yaitu :
- Branch yang artinya membangun semua cabang tree yang mungkin menuju solusi.
- Bound yang artinya menghitung node mana yang merupakan active node (E-node) dan node mana yang merupakan dead node (D-node) dengan menggunakan syarat batas constraint (kendala). Digunakan untuk persoalan optimisasi → meminimalkan atau memaksimalkan suatu fungsi objektif, yang tidak melanggar batasan (constraints) persoalan
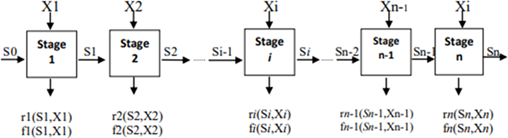
Dynamic programming dapat didefinisikan sebagai suatu pendekatan matematik yang memiliki prosedure sistematis yang dirancang sedemikian rupa dengan tujuan untuk mengoptimalkan penyelesaian suatu masalah tertentu yang diuraikan menjadi sub-sub masalah yang lebih kecil yang terkait satu sama lain dengan tetap memperhatikan kondisi dan batasan permasalahan tersebut. Struktur dynamic programming untuk dapat dimengerti secara lebih jelas dan lebih spesifik, umumnya dideskripsikan dengan suatu sistem notasi. Struktur dynamic programming disebut juga dengan model dynamic programming. Notasi dan simbol yan digunakan dalam model dynamic programming adalah beragam, namun secara umum dapat dinyatakan sebagai berikut : i = Tahap keputusan ke - i. n = Banyak tahap keputusan. Xi = Variable keputusan pada tahap keputusan ke – i. Si(Si – 1, Xi) = Status pada tahap keputusan ke – i. ri(Si,Xi) = Return pada tahap keputusan ke – i. fi(Si,Xi) = Nilai keputusan pada tahap keputusan ke – i, untuk status Si dan variable keputusan Xi. fi*(Si) = Nilai keputusan optimal pada tahap keputusan ke – i, untuk status Si.
Pada umumnya dynamic programming digunakan untuk masalah optimisasi. Dimana suatu permasalahan memiliki banyak solusi. Setiap solusi memiliki nilai masing-masing dan ingin ditemukan solusi dengan nilai yang optimum (maksimal atau mininal). Dynamic programming dapat dibagi menjadi empat tahap yang berurutan sebagai berikut :
- Karakterisasi struktur pada solusi optimasi
- Mendefinisikan nilai solusi optimal secara rekursif
- Menghitung nilai solusi optimal pada model bottom-up
- Menyusun solusi optimal dari informasi hasil perhitungan