Multi-Object Tracking (MOT)

Multi-Object Tracking is a task in computer vision that involves detecting and tracking multiple objects within a video sequence.

The goal is to identify and locate objects of interest in each frame and then associate them across frames to keep track of their movements over time.

This task is challenging due to factors such as occlusion, motion blur, and changes in object appearance, and is typically solved using algorithms that integrate object detection and data association techniques.

This MOT component provides the following features:

Provides 7 different trackers which are released from the year 2016 - 2023.
Easy to integrate various MOT trackers with the object detection algorithm of your choice.
The reference code of the trackers has been modified so as to provide the same output format no matter which tracker you use.

Directory and files information:-

data -> contains the sample data.
detectors -> contains the object detection class definition.
notebooks -> contains the jupyter notebook.
trackers -> contains the various trackers class definitions.
utils -> contains the utility functions.
requirements.txt -> contains the library dependency requirements.

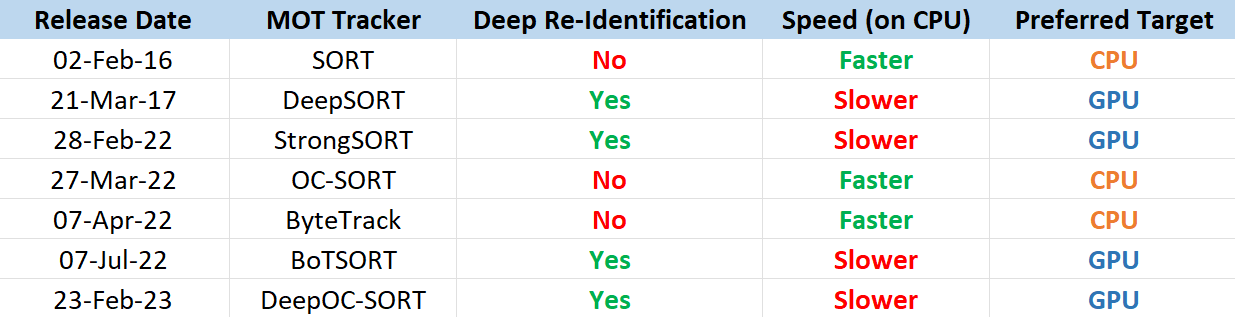
Below is a table that gives the information about the 7 MOT trackers that this component provides (ordered by release date).

Note: Deep Re-Identification means the respective trackers make use of a deep learning model like ResNet18 or MobileNetV2 to calculate the features of the objects across the frames, which is later used to measure the similarity between these features.

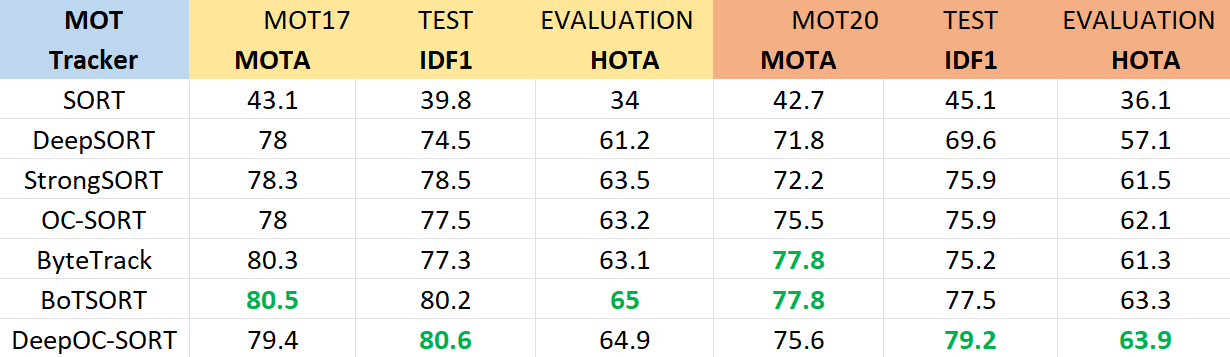
Below table shows the standard MOT17 and MOT20 Test Evaluation results of these trackers using evaluation metrics - Multi-Object Tracking Accuracy(MOTA), Identification-F1(IDF1), Higher-Order Tracking Acuracy(HOTA)

Experimentation

An experimentation is carried out on the pedestrians video with the following information:

Target device = CPU
Processor = 11th Gen Intel(R) Core(TM) i5-1135G7 @ 2.40GHz 1.38GHz
Object Detector = YoloV8 Nano (yolov8n.pt)
Video source = https://www.youtube.com/watch?v=EXUQnLyc3yE (starts @ 0.39 seconds)
Video size = 640 x 360
Total number of frames = 882

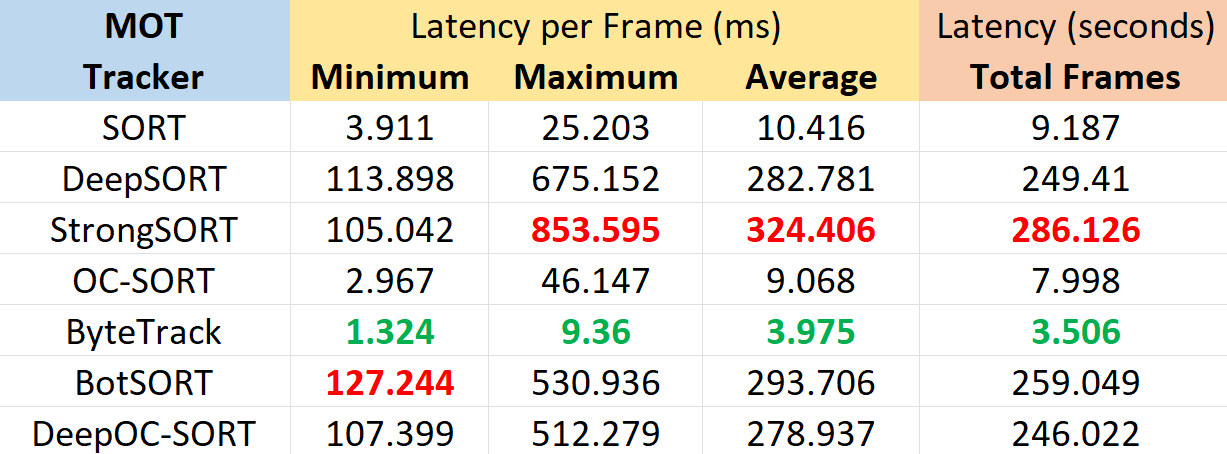
Below tables gives information about the results of the experimentation performed using various MOT trackers.

Note that, the latencies in the above table are just with respect to various MOT trackers and it does not consider the latencies of the end-to-end tracking process that includes object detection as primary task.

Points to Remember:

Even a highly accurate MOT tracker is meaningless if the Object Detection algorithms performs poor.
To build a good the tracking system, it is important to optimize the Object Detection model and the Deep ReID model (if the MOT tracker uses it). This leads to more FPS gains and less latency of overall tracking system.

Please read the following to understand how the Multi-Object Tracking actually works.

First, lets understand the 2 components, namely, Kalman Filter and Hungarian Algorithm.

1) Kalman Filter (KF)

Kalman Filter is an algorithm that provides estimates of some unknown variables given the measurements observed over time. They have been demonstrating its usefulness in various applications including rockets. Kalman filters have relatively simple form and require small computational power.
Now with respect to Object Detection, given an input frame at time T and a bounding box detection of an object, the Kalman Filter (at time T) estimates the the position of the bounding box of that object for time (T + 1). i.e. at current frame it estimates the bounding box coordinates for the next frame.

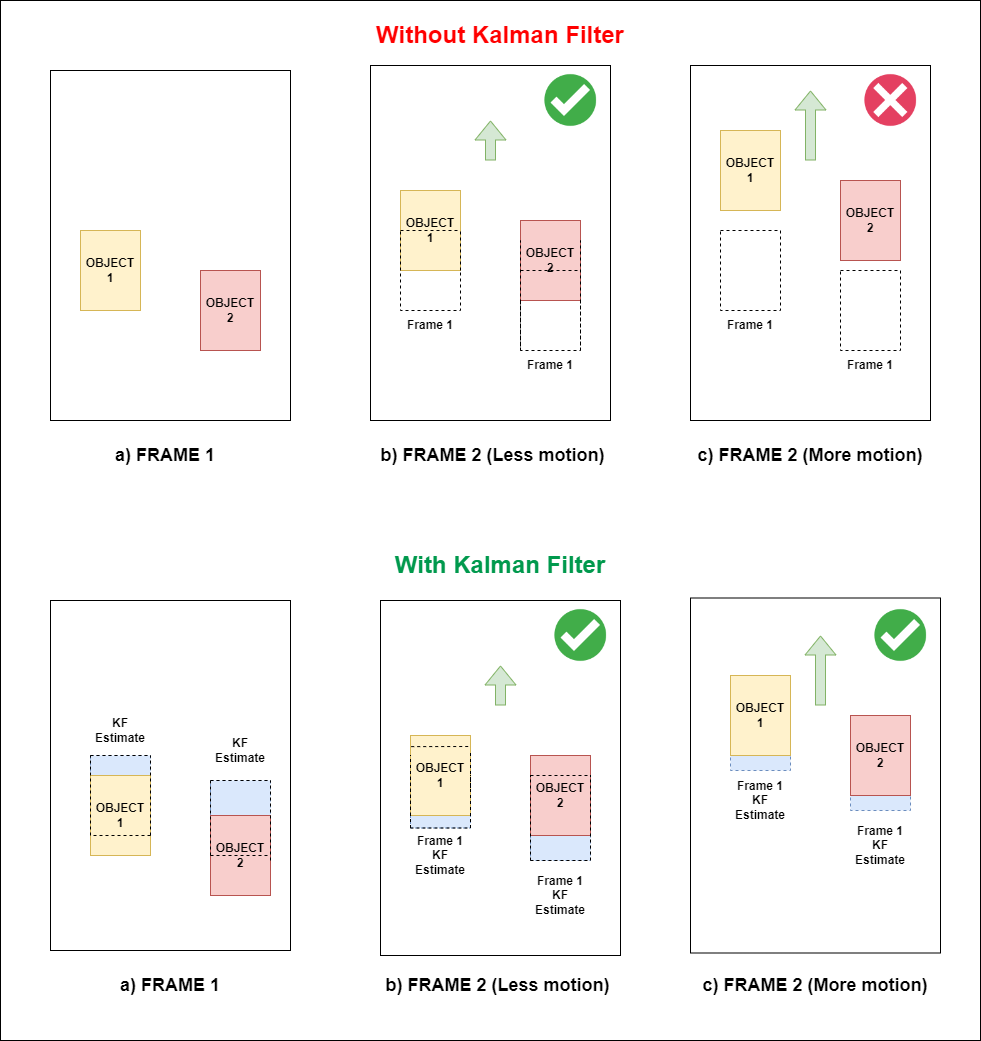
Let us understand how this is actually helpful through the following diagram.

Consider the IOU threshold value = 0.5.

1.a) Without Kalman Filter:

a) Frame 1 - consider this frame at time T where it has 2 detected objects.
b) Frame 2 (Less motion) - consider this frame at time (T+1) where objects position is changed due to less motion. Now if we compare the IOUs of these 2 objects between current frame (T+1) and previous frame (T). The Object 1 IOU = 0.5 and Object 2 IOU is < 0.5. As IOU threshold is 0.5, Object 1 is considered as same object instance but Object 2 is not considered as the same object instance, across the frames.
c) Frame 2 (More motion) - consider this frame at time (T+1) where objects position is changed due to more motion. Now if we compare the IOUs of these 2 objects between current frame (T+1) and previous frame (T). The IOUs are = 0.0. Thus, there are zero chances of these 2 objects to be considered as the same object instance(s) across the frames.

1.b) With Kalman Filter:

a) Frame 1 - consider this frame at time T where it has 2 detected objects.
b) Frame 2 (Less motion) - consider this frame at time (T+1) where objects position is changed due to less motion. Now if we compare the IOUs of these 2 objects between current frame (T+1) and previous frame (T) (instead of detected bounding box of previous frame we now consider the KF bounding box estimate). The IOUs for both the Objects is >= 0.5. Thus, there are more chances of these 2 objects to be considered as the same object instance(s) across the frames.
c) Frame 2 (More motion) - consider this frame at time (T+1) where objects position is changed due to more motion. Now if we compare the IOUs of these 2 objects between current frame (T+1) and previous frame (T) (instead of detected bounding box of previous frame we now consider the KF bounding box estimate). The IOUs are >= 0.5. Thus, there are more chances of these 2 objects to be termed as the same object instance(s) across the frames

Isn't Kalman Filter an amazing algorithm? It assumes the constant velocity model and estimates the next state based on the previous state, thus if there is increase/decrease in motion at frame (T+1), then it means that at frame T, the change in motion is comparatively less which makes sense due to the fact that the motion increases/decreases linearly across the frames.

2) Hungarian Algorithm

The Hungarian algorithm or Hungarian matching algorithm, also called the Linear Assignment Problem, is an algorithm that can be used to find maximum-weight matchings in bipartite graphs (a set of graph vertices decomposed into two disjoint sets such that no two graph vertices within the same set are adjacent).
Now with respect to Object Detection, it decomposes all the bounding boxes (i.e. KF estimated bounding boxes(for frame T+1) at frame T & detected bounding boxes at frame (T+1)) into 2 disjoint sets, such that KF estimated bounding boxes at frame T belong to one set and detected bounding boxes at frame (T+1) belong to a different set. The term "maximum-weight" here can be a metric like IOU, cosine similarity or distance, etc

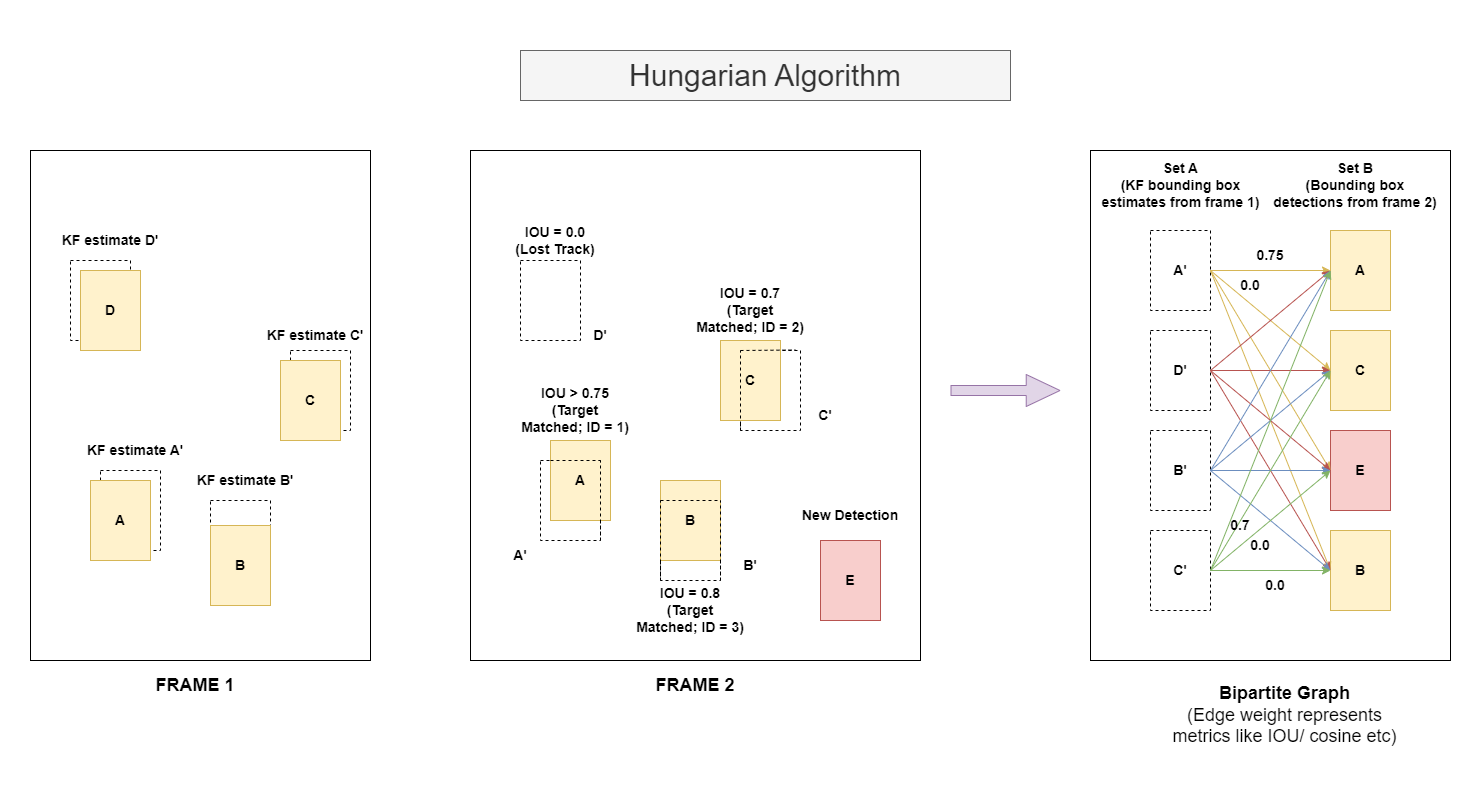
Let us visually understand how it actually helps in associating the target bounding boxes at time (T+1).

Considering the above figure, Frame 1 represents the detected bounding boxes [A,B,C,D] with their respective KF bounding box estimates [A',B',C',D'] at time T and the frame 2 represents the detected bounding boxes [A,B,C,E] at time (T+1) and the KF bounding box estimates [A',B',C',D'] from time T.
Notice how the detection of bounding box D is lost in the frame 2 -> possible reasons - either the object D is not at all available in the frame 2 or the object detection algorithm failed to detect due to the poor confidence score/ occlusion. Also, there is a new object E got detected.
Figure also shows the Bipartite graph where all the detections are decomposed into 2 sets. The edges represents the metric like IOU as an example.
The Bipartite graph gives information that the cost A' to A is maximum among all the cost pairs ([A', A],[A',C],[A',E],[A',B]), Thus, across the frame, we can say that the A' and A, both are the same object instances.
Similarly, same process is performed for all the bounding box pairs between these 2 sets (refer the above figure).

Note: Hungarian Algorithm is used for just matching the boxes pairs. But MOT algorithms keeps track of KF bounding box estimates from previous frames and detected objects from current frame. Thus, it knows if the unmatched bounding box is a new detected object at frame (T+1) or a undetected (occlusion/ poor confidence score/ object is not available in the frame) object from frame T.

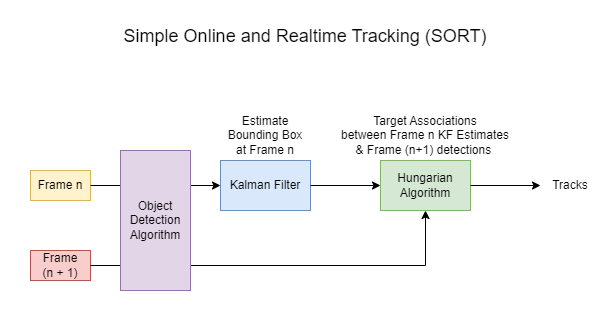
High-level diagram of a Simple Online and Realtime Tracking (SORT) algorithm which revolutionarized the Multi-Object Tracking.

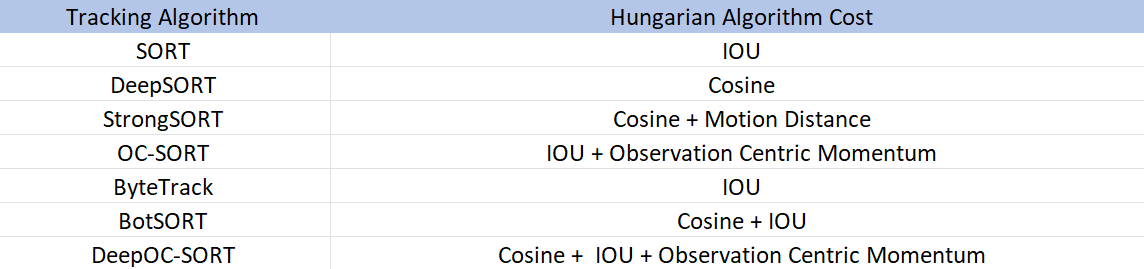
Please find the below table that describes the Cost for the Hungarian Algorithm used by various MOT trackers.

Note:

The cosine cost means the respective tracker uses a deep learning model to compute the features of the bounding box object.
The cost metrics is not the only thing that makes other trackers different from SORT.
Apart from just using the different cost metrics, various trackers use various algorithms or approaches to track the matched tracks, unmatched tracks, lost tracks and etc., that is how these trackers have achieved State-of-the-Art (SOTA) results on MOT17 and MOT20 test evaluation datasets as of 2023.

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

Repository files navigation